maria alejandra baron

Temas del Álgebra

    Expresiones algebraicas

    Operaciones Algebraicas con polinomios 

     Productos Notables

EXPRESIONES ALGEBRAICAS

Una expresión algebraica es un conjunto de cantidades numéricas y literales relacionadas entre sí­ por los signos de las operaciones aritméticas como sumas, diferencias, multiplicaciones, divisiones, potencias y extracción de raí­ces.

Algunos ejemplos de expresiones algebraicas son:

       o       

Si x es una variable, entonces un monomio en x es una expresión de la forma axⁿ, en donde a es un numero real y n es un entero no negativo.   Un binomio es la suma de dos monomios que no se pueden simplificar y un trinomio es la suma de tres monomios que no se pueden simplificar.

monomio	binomio	trinomio

Recuerda siempre que un monomio tiene solo un término, un binomio dos términos y un trinomio tres términos.

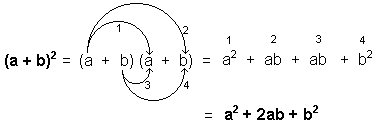
Operaciones Algebraicas con polinomios

Definición:   Un polinomio en x es una suma de la forma: an xn + an-1 xn-1 + ··· + a2 x2 + a1 x + a0 Donde n es un entero no negativo y cada coeficiente de x es un numero real. Si an es un numero diferente de cero, se dice que el polinomio es de grado n.

El coeficiente a de la mayor potencia de x es el coeficiente principal del polinomio.

Ejemplos de polinomios:

Ejemplo	Coeficiente principal	Grado
	3	4
	1	8
	-5	2
8	8	0
	7	1

Ejemplos de expresiones que no son polinomios:

               a)                                           b)                             c) 

En el primer ejemplo el exponente de es negativo   contradiciendo la definición de polinomio, de igual forma en el ejemplo c donde el exponente de   no es entero.

En el ejemplo b tenemos una expresión racional o fraccionaria con un polinomio en el numerador y otro en el denominador. El criterio que utilizaremos es el siguiente si el polinomio del denominador no es el   constante o de grado cero, la expresión no es un polinomio. Recuerde que los exponentes deben ser enteros positivos.

Productos notables

Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llamanfactores.

Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saberfactorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.

Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.

 A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).

Cuadrado de la suma de dos cantidades o binomio cuadrado

a2 + 2ab + b2 = (a + b)2

El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.

Demostración:

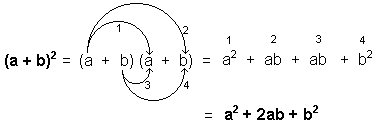
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a² + 2ab + b² debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)²

EXTRAÍDO DE :
http://quiz.uprm.edu/tutorials/ea/ea_home.html
http://www.profesorenlinea.cl/matematica/AlgebraProductosnotables.htm