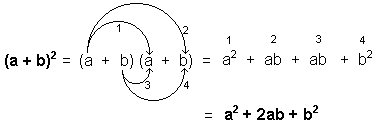MARIA ALEJANDRA BARON Y VANESSA PATIÑO

VIDEOS

Estadistica

ESTADISTICA

ESTADISTICA

GEOMETRIA

GEOMETRIA

GEOMETRIA

Vanessa Patiño

¿Que es la Geometría?

La geometría es una parte de la matematica que trata de estudiar unas idealizaciones del espacio en que vivimos, que son los puntos, las rectas y los planos, y otros elementos conceptuales derivados de ellos, como poligonos o poliedros.

En la practica, la geometría sirve para solucionar problemas concretos en el mundo de lo visible. Entre sus utilidades se encuentran la justificación teorica de muchos instrumentos: compás, teodolito, pantógrafo, sistema de posicionamiento global. También es la que nos permite medir areas y volumenes, es útil en la preparación de diseños, e incluso en la fabricación de artesanías.

La geometria clásica o axiomática es una matemática en la cuál los objetos, en vez de ser números, son puntos, rectas, planos y otras figuras definidas en función de estas.

Ángulos

Los ángulos miden la cantidad de giro

Nombres de los ángulos

Según aumenta el ángulo, el nombre va cambiando

Tipos de ángulos	Descripción
Ángulo agudo	un ángulo de menos de 90°
Ángulo recto	un ángulo de 90°
Ángulo obtuso	un ángulo de más de 90° pero menos de 180°
Ángulo llano	un ángulo de 180°
Ángulo reflejo o cóncavo	un ángulo de más de 180°

Cuidado con las medidas

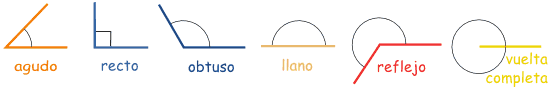
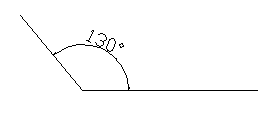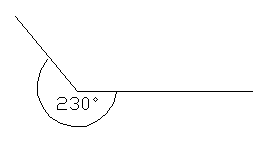
Este ángulo es obtuso.	Este ángulo es reflejo.
Pero las líneas son las mismas... así que cuando midas y marques ángulos, ¡asegúrate de que sabes cuál de los ángulos necesitas!

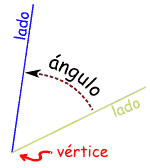Partes de un ángulo La esquina de un ángulo se llama vértice Y los lados rectos son rayos El ángulo es la cantidad de giro entre los dos rayos.

Marcar ángulos

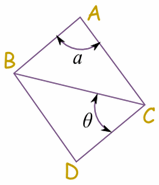
Hay dos maneras comunes de marcar un ángulo: 1. dándole nombre, normalmente una letra minúscula como a o b, o a veces una letra griega como α (alfa) o θ (theta) 2. o con las tres letras que definen el ángulo, poniendo en medio la letra donde se encuentra (su vértice). Ejemplo: el ángulo "a" es "BAC", y el ángulo "θ" es "BCD" EXTRAÍDO DE : http://www.culturageneral.net/matematicas/definicion_geometria.htm http://www.disfrutalasmatematicas.com/geometria/angulos.html

MARIA ALEJANDRA BARON Y VANESSA PATIÑO

VIDEO

ALGEBRA

EXPRESIONES ALGEBRAICAS

OPERACIONES ALGEBRAICAS CON POLINOMIOS

PRODUCTOS NOTABLES

Estadística

 

Geometría 

Maria alejandra baron

Graficos de estadistica

Los gráficos son medios popularizados y a menudo los más convenientes para presentar datos, se emplean para tener una representación visual de la totalidad de la  información. Los gráficos estadísticos presentan los datos en forma de dibujo de tal modo que se pueda percibir fácilmente los hechos esenciales y compararlos con otros. 

Tipos de gráficos estadísticos

• Barras
• Líneas
• Circulares
• Áreas
• Histogramas
• otros
•  DIAGRAMA DE BARRAS
• 
• LINEAS
• 
• CIRCULARES
• 
• ÁREAS
• 
• HISTOGRAMA
• 
• EXTRAIDO DE :
• http://html.rincondelvago.com/graficos-estadisticos.htmlhttps://www.google.com.co/search?q=estadistica&espv=2&biw=1366&bih=667&source=lnms&tbm=isch&sa=X&ei=Oo5LVZqlN4uxggS0vYHABQ&ved=0CAYQ_AUoAQ#tbm=isch&q=histograma+estadistica%2B&imgrc=cGoGbs0ganfQUM%253A%3B8XqCnRqd7_qHgM%3Bhttp%253A%252F%252Fupload.wikimedia.org%252Fwikipedia%252Fcommons%252Fthumb%252F8%252F8e%252FHistogram_example.svg%252F250px-Histogram_example.svg.png%3Bhttp%253A%252F%252Fes.wikipedia.org%252Fwiki%252FHistograma%3B250%3B200
• 
  

Vanessa Patiño

¿Que es la estadística?

  La estadística es la parte de las matemáticas que se ocupa de los métodos para recoger, organizar, resumir y analizar datos, así como para sacar conclusiones válidas y toma decisiones razonables basadas en tal análisis.

En la antigüedad los egipcios hacían censos de las personas y de los bienes inmuebles que permitían conocer la distribución de las propiedades para volver a restituir los después de la inundación anual que provoca el río Nilo. En la biblia hay referencias a censos del pueblo judío. Los griegos y los romanos hacían censos de personas y de propiedades.                                   
extraído de :
http://www.ceibal.edu.uy/contenidos/areas_conocimiento/mat/estadistica/qu_es_la_estadstica.html
https://www.google.com.co/search?q=estadistica&espv=2&biw=1366&bih=667&source=lnms&tbm=isch&sa=X&ei=Oo5LVZqlN4uxggS0vYHABQ&ved=0CAYQ_AUoAQ#imgrc=3y0Dp7tyOwdd_M%253A%3BVQk6B7hbzUcbEM%3Bhttp%253A%252F%252Fcienciascsjic.files.wordpress.com%252F2013%252F11%252Festadistica.jpg%3Bhttp%253A%252F%252Flaperspectivadelpoliedro.blogspot.com%252F2015%252F01%252Fla-diosa-estadistica.html%3B2530%3B1582

maria alejandra baron

Temas del Álgebra

    Expresiones algebraicas

    Operaciones Algebraicas con polinomios 

     Productos Notables

EXPRESIONES ALGEBRAICAS

Una expresión algebraica es un conjunto de cantidades numéricas y literales relacionadas entre sí­ por los signos de las operaciones aritméticas como sumas, diferencias, multiplicaciones, divisiones, potencias y extracción de raí­ces.

Algunos ejemplos de expresiones algebraicas son:

       o       

Si x es una variable, entonces un monomio en x es una expresión de la forma axⁿ, en donde a es un numero real y n es un entero no negativo.   Un binomio es la suma de dos monomios que no se pueden simplificar y un trinomio es la suma de tres monomios que no se pueden simplificar.

monomio	binomio	trinomio

Recuerda siempre que un monomio tiene solo un término, un binomio dos términos y un trinomio tres términos.

Operaciones Algebraicas con polinomios

Definición:   Un polinomio en x es una suma de la forma: an xn + an-1 xn-1 + ··· + a2 x2 + a1 x + a0 Donde n es un entero no negativo y cada coeficiente de x es un numero real. Si an es un numero diferente de cero, se dice que el polinomio es de grado n.

El coeficiente a de la mayor potencia de x es el coeficiente principal del polinomio.

Ejemplos de polinomios:

Ejemplo	Coeficiente principal	Grado
	3	4
	1	8
	-5	2
8	8	0
	7	1

Ejemplos de expresiones que no son polinomios:

               a)                                           b)                             c) 

En el primer ejemplo el exponente de es negativo   contradiciendo la definición de polinomio, de igual forma en el ejemplo c donde el exponente de   no es entero.

En el ejemplo b tenemos una expresión racional o fraccionaria con un polinomio en el numerador y otro en el denominador. El criterio que utilizaremos es el siguiente si el polinomio del denominador no es el   constante o de grado cero, la expresión no es un polinomio. Recuerde que los exponentes deben ser enteros positivos.

Productos notables

Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llamanfactores.

Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saberfactorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.

Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios.

 A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable).

Cuadrado de la suma de dos cantidades o binomio cuadrado

a2 + 2ab + b2 = (a + b)2

El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a² + 2ab + b² debemos identificarla de inmediato y saber que podemos factorizarla como (a + b)²

EXTRAÍDO DE :
http://quiz.uprm.edu/tutorials/ea/ea_home.html
http://www.profesorenlinea.cl/matematica/AlgebraProductosnotables.htm

Maria Alejandra Baron

Ecuaciones del Álgebra